Dynamic Effects on Hospitalization
Setting
We follow Dobkin et al. (2018) in estimating the causal effect of hospital admissions on out-of-pocket medical spendings.1 This application is instructive in that it illustrates how DML can be used for difference-in-difference analyses. The analysis of Dobkin et al. (2018) was reconsidered by Sun & Abraham (2021) to illustrate their proposed DiD estimator.
The demonstration here is a simplified version of the analysis presented in Section 5 of our review paper. For the full replication code, see our replication repository (Link to be added).
The variables used are:
| Variable | Description |
|---|---|
oop_spend | Out of pocket medical expenditures prev 12 months |
first_hosp | First hospitalization |
hhidpn | Household/person indicator |
wave | Wave indicator |
ragey_b | Age in years |
female | Female indicator |
black | Black indicator |
hispanic | Hispanic indicator |
race_other | Other race |
hs_grad | High school graduate |
some_college | College degree |
collegeplus | Higher than college education |
Data and model set-up
We begin by loading the data, and specifying settings for a number of nuisance function estimators that we will use below. We consider OLS/logit as parametric reference specifications, (logistic) lasso and ridge, and three random forest learners.
R code
Note that for the DiD analyses to run in R, you will need to install a modified version of the original did package by Callaway & Santa’Anna.
# Hard-coded hyperparameters
library("did")
#devtools::install_github("thomaswiemann/did",ref="dev-ddml")
library(ddml)
library(readr)
dat <- read_csv("https://dmlguide.github.io/assets/dta/HRS_long.csv")
# Learners for E[Y|D=0,X] estimation
learners = list(
list(fun = ols),
list(fun = mdl_glmnet,
args = list(alpha = 1)),
list(fun = mdl_glmnet,
args = list(alpha = 0)),
list(fun = mdl_ranger,
args = list(num.trees = 1000, # random forest, high regularization
min.node.size = 100)),
list(fun = mdl_ranger,
args = list(num.trees = 1000, # random forest, medium regularization
min.node.size = 10)),
list(fun = mdl_ranger,
args = list(num.trees = 1000, # random forest, low regularization
min.node.size = 1)))
# Hard-code learners for treatment reduced-form
learners_DX = list(
list(fun = mdl_glm,
args = list(family = "binomial")),
list(fun = mdl_glmnet,
args = list(family = "binomial", # logit-lasso
alpha = 1)),
list(fun = mdl_glmnet,
args = list(family = "binomial", # logit-ridge
alpha = 0)),
list(fun = mdl_ranger,
args = list(num.trees = 1000, # random forest, high regularization
min.node.size = 100)),
list(fun = mdl_ranger,
args = list(num.trees = 1000, # random forest, medium regularization
min.node.size = 10)),
list(fun = mdl_ranger,
args = list(num.trees = 1000, # random forest, low regularization
min.node.size = 1)))
DiD estimation with parametric nuisance functions
For comparison, we employ the Callway & Sant’Anna estimator of group-time average treatment effects (GT-ATT). Each GT-ATT corresponds to the ATT of a hospitalization occuring at time $g$ on out-of-pocket medical spending at time $t$. We also consider the Sant’Anna & Zhao (2020) estimator that adjust for covariates using a doubly robust scores. Unlike DML, their estimator does not employ sample-splitting and assumes that the nuisance functions follow a parameteric form.
The GT-ATT estimates are then aggregated to obtain dynamic effects for up to two periods before and after the treatment onsets.
R code
# Without controls
attgt_0 <- att_gt(yname = "oop_spend",
gname = "first_hosp",
idname = "hhidpn",
tname = "wave",
control_group = "notyettreated",
xformla = NULL,
data = dat,
bstrap=FALSE)
# Aggregation
dyn_0 <- aggte(attgt_0, type = "dynamic", bstrap = FALSE)
# With controls
attgt_lm <- att_gt(yname = "oop_spend",
gname = "first_hosp",
idname = "hhidpn",
tname = "wave",
control_group = "notyettreated",
xformla = ~ ragey_b+ragey_b^2+ragey_b^3+female+black+
hispanic+race_other+hs_grad+some_college+collegeplus,
data = dat,
bstrap=FALSE,
est_method = "dr",
learners = list(list(fun = ols)),
learners_DX = list(list(fun = mdl_glm,
args = list(family = binomial))),
type = "average",
trim = 0.001)
# Aggregation
dyn_lm <- aggte(attgt_lm, type = "dynamic", bstrap = FALSE)
R output
> attgt_0
Call:
att_gt(yname = "oop_spend", tname = "wave", idname = "hhidpn",
gname = "first_hosp", xformla = NULL, data = dat, control_group = "notyettreated",
bstrap = FALSE)
Reference: Callaway, Brantly and Pedro H.C. Sant'Anna. "Difference-in-Differences with Multiple Time Periods." Journal of Econometrics, Vol. 225, No. 2, pp. 200-230, 2021. <https://doi.org/10.1016/j.jeconom.2020.12.001>, <https://arxiv.org/abs/1803.09015>
Group-Time Average Treatment Effects:
Group Time ATT(g,t) Std. Error [95% Pointwise Conf. Band]
8 8 3028.6250 913.4765 1238.2440 4819.006 *
8 9 1247.6922 860.7461 -439.3392 2934.724
8 10 800.1065 1007.5356 -1174.6271 2774.840
9 8 -169.9604 1128.4012 -2381.5861 2041.665
9 9 3324.3702 958.7806 1445.1947 5203.546 *
9 10 106.8378 650.6511 -1168.4149 1382.091
10 8 37.8749 1403.3889 -2712.7167 2788.467
10 9 -410.5810 1027.0575 -2423.5767 1602.415
10 10 3091.5084 995.4291 1140.5031 5042.514 *
---
Signif. codes: `*' confidence band does not cover 0
P-value for pre-test of parallel trends assumption: 0.94949
Control Group: Not Yet Treated, Anticipation Periods: 0
Estimation Method: Doubly Robust
Stata code (to be added)
To be added.
Stata output (to be added)
To be added.
Double Machine Learning DiD estimation
We move to the DML estimation. The code uses the same doubly robust (and Neyman-orthogonal) score as Sant’Anna & Zhao (2020) to estimate the GT-ATT effects. However, DML uses cross-fitting which (in combination with the Neyman-orthogonal score) allows us to leverage nonparametric learners.
R code
attgt_dml <- att_gt(yname = "oop_spend",
gname = "first_hosp",
idname = "hhidpn",
tname = "wave",
control_group = "notyettreated",
xformla = ~ ragey_b+female+black+
hispanic+race_other+hs_grad+some_college+collegeplus,
data = dat,
bstrap=FALSE,
est_method = "ddml",
learners=learners,
learners_DX=learners_DX,
ensemble_type="nnls",
sample_folds=15,
shortstack=TRUE,
trim = 0.001,
silent=FALSE)
dyn_dml <- aggte(attgt_dml, type = "dynamic", bstrap = FALSE)
Stata code (to be added)
To be added.
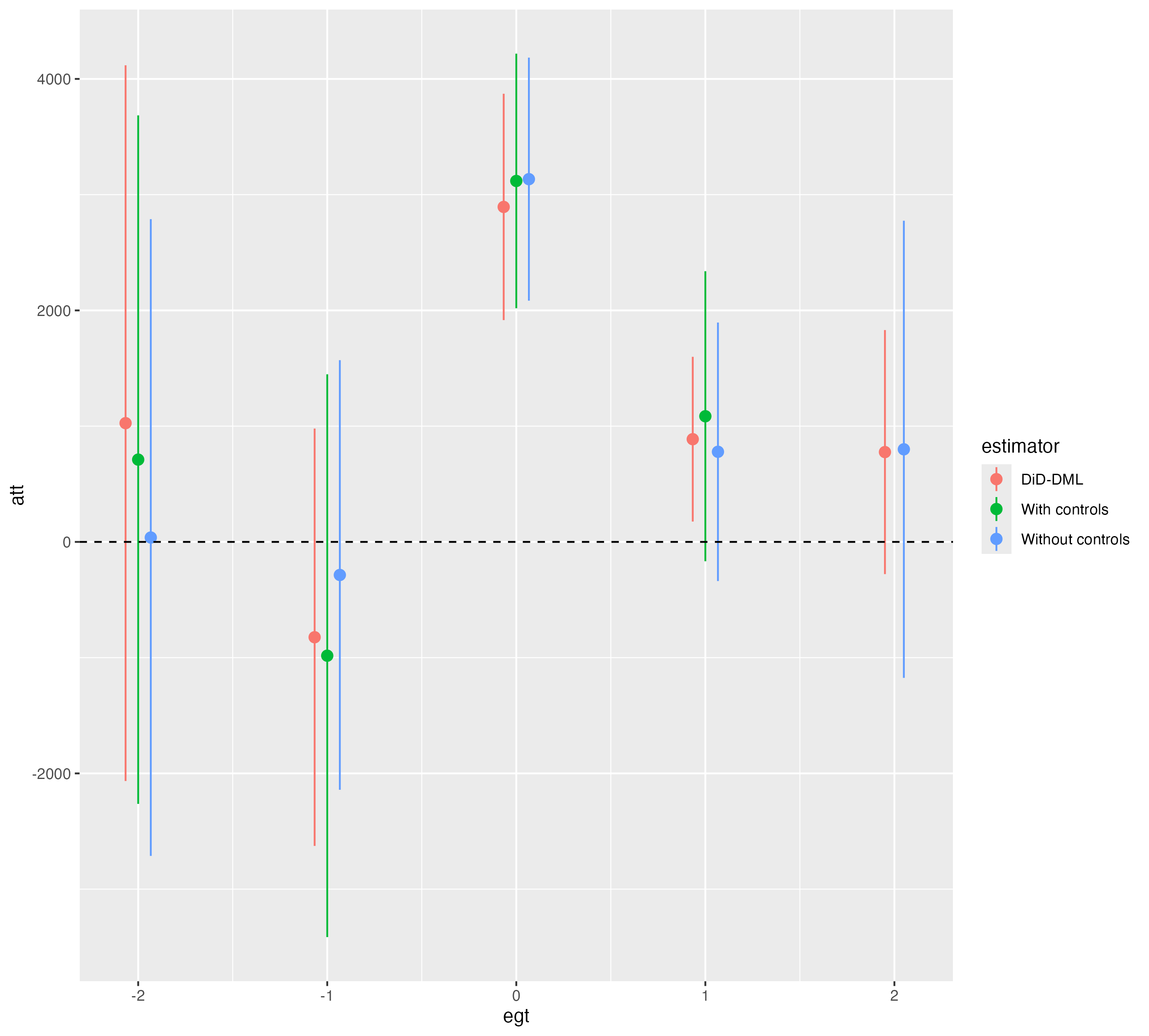
Results
Finally, we prepare a plot to display the results:
R results
res <- bind_rows(
data.frame(egt=dyn_dml$egt,att=dyn_dml$att.egt,se=dyn_dml$se.egt,estimator="DiD-DML"),
data.frame(egt=dyn_lm$egt,att=dyn_lm$att.egt,se=dyn_lm$se.egt,estimator="With controls"),
data.frame(egt=dyn_0$egt,att=dyn_0$att.egt,se=dyn_0$se.egt,estimator="Without controls")
)
res |>
ggplot() +
geom_pointrange(aes(x=egt,y=att,
ymin=att-1.96*se,ymax=att+1.96*se,
color=estimator),position=position_dodge(width=0.2)) +
geom_hline(yintercept=0,linetype="dashed")
Stata results (to be added)
To be added.
-
The full data is available from the OpenICPSR repository. We consider here the subset of the data that that was also considered by Sun & Abraham (2021). ↩