Understanding Cultural Persistence and Change
Setting
In this example, we illustrate DML estimation of the partially linear model using a simple empirical example. The application is drawn from Giuliano and Nunn (2021), who look at the relationship between climate instability and cultural persistence using a number of different datasets.
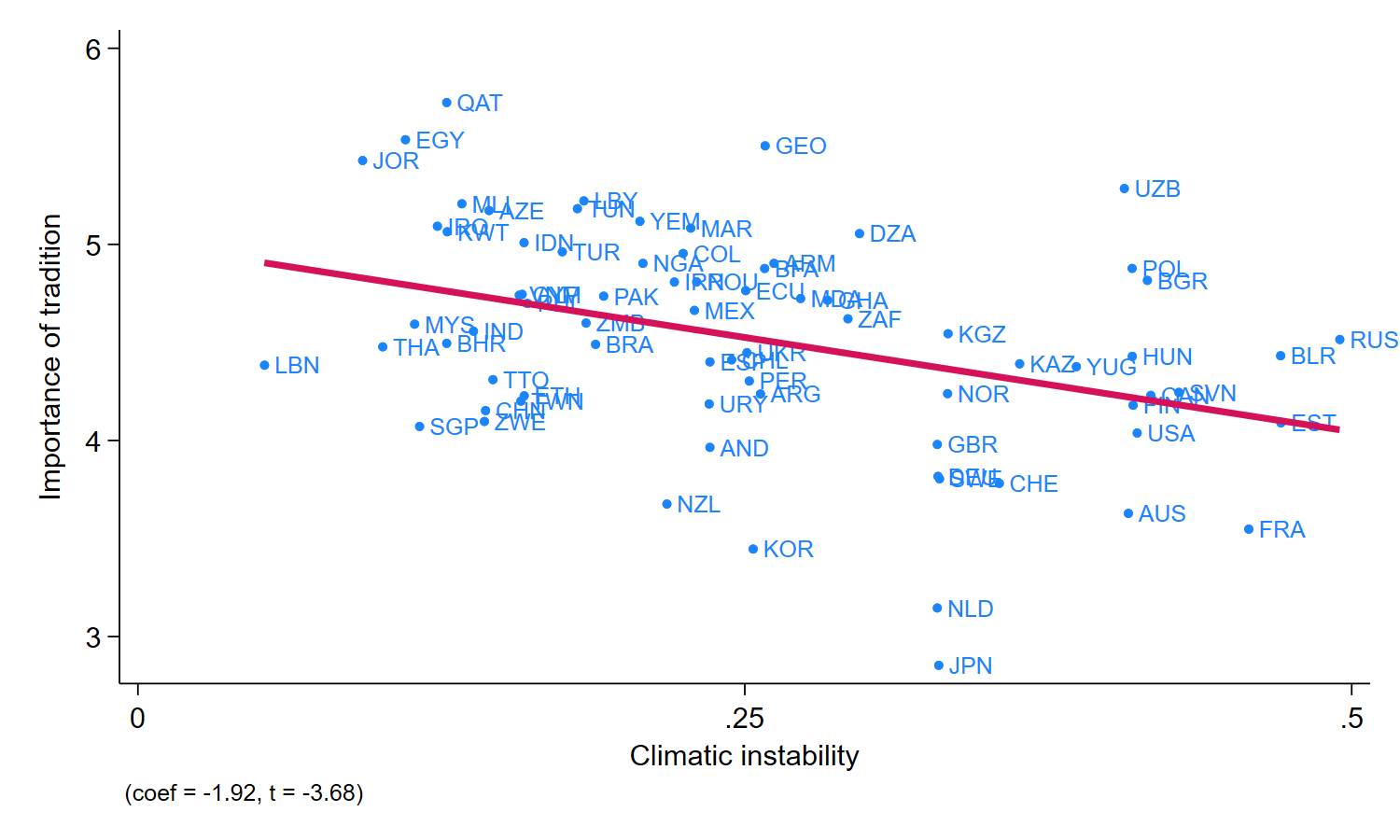
Their first estimation is a cross-country regression where the dependent variable, $Y$, is a measure of the importance of tradition taken from the World Values Survey, and the causal variable of interest, $D$, is a measure of ancestral climatic instability. The dataset is quite small: only 74-75 countries.
The example is useful for illustrating how DML works for several reasons: the dataset is small and available online, visualization is easy, reproduction of results is straightforward, and the example shows how DML can be used as a robustness check even in the simplest of settings. The G-N dataset used for this demonstration is available here.
Giuliano and Nunn (G-N) are concerned about omitted confounders, and include 4 controls to address the issue. The outcome, treatment and control variables are:
| Variable | Description |
|---|---|
A198new | The outcome variable of interest: country-level average of the self-reported importance of tradition. Ranges from 1 to 6 (bigger=more important). |
sd_EE | The causal variable of interest: a measure of ancestral climatic instability (standard deviation of temperature anomaly measure across generations; see G-N for details). |
v104_ee | Control #1: distance from the equator. |
settlement_ee | Control #2: early economic development (proxied by complexity of settlements). |
polhierarchies_ee | Control #3: political hierarchies (a measure of political centralization). |
loggdp | Control #4: log GDP per capita in the country of origin at the time of the survey. |
Their model with controls is one where the controls enter linearly and is estimated using OLS. The effect of climatic instability on the importance of tradition is negative, with a coefficient that is different from zero at conventional significance levels.
G-N summarize as follows (p. 155):
Based on the estimates from column 4, a one-standard-deviation increase in cross-generational instability (0.11) is associated with a reduction in the tradition index of 1.824×0.11=0.20, which is 36% of a standard deviation of the tradition variable.
Replication
We first reproduce, with the help of G-N’s replication code, columns (3) and (4) in Table 1 of the published paper. Column (3) is a bivariate linear regression of the outcome $Y$ (importance of tradition) on the causal variable of interest $D$ (ancestral climatic instability). Column (4) has the OLS results when the 4 controls are included. In the DML example below, we show how to use DML to estimate the Column (4) specification.
We also reproduce their replication code for Figure 5, which is a simple scatterplot of the bivariate regression with no controls reported in Column (3).
Stata code
use "https://dmlguide.github.io/assets/dta/GN2021.dta", clear
// shorten the name of the causal variable of interest to sd_EE
rename sd_of_gen_mean_temp_anom_EE sd_EE
// replicate results with no controls in Table 1, column (3).
eststo m0: ///
reg A198new sd_EE, robust
// replicate Figure 5
reg A198new sd_EE, robust
predict hat
twoway (scatter A198new sd_EE, msymbol(o) mlabel(isocode)) ///
(line hat sd_EE, sort lwidth(thick)), ///
legend(off) xlabel(0 0.25 0.5, nogrid) ///
ylabel(3 4 5 6, nogrid) ///
note("(coef = -1.92, t = -3.68)") ///
ytitle("Importance of tradition") ///
xtitle("Climatic instability")
drop hat
graph export "logs/GN_Figure5.png", replace
// replicate results with controls in Table 1, column (4).
eststo m1: ///
reg A198new sd_EE v104_ee settlement_ee polhierarchies_ee loggdp, robust
Stata output
. esttab m0 m1
--------------------------------------------
(1) (2)
A198new A198new
--------------------------------------------
sd_EE -1.923*** -1.824*
(-3.68) (-2.62)
v104_ee 0.00542
(1.01)
settlemen~ee -0.0651
(-1.87)
polhierar~ee 0.0128
(0.13)
loggdp -0.165**
(-3.39)
_cons 5.006*** 6.576***
(35.91) (12.27)
--------------------------------------------
N 75 74
--------------------------------------------
R code (to be added)
R output here
R output (to be added)
R output here
DML as a robustness check
A useful robustness check is to ask whether the results with controls are sensitive to the assumption that the controls enter linearly. DML can help answer this question. Below we estimate the model with controls using DML and the partially-linear model (PLM). The specification is still very simple: we keep the assumption that the controls enter separately, but drop linearity.
The estimation procedure takes the following steps:
- Specify the DML model: in this case, the PLM.
- Specify the learners: choose the learners for the conditional expectation functions for the outcome variable and the causal variable of interest.
- Cross-fitting: obtain cross-fit estimates of the two conditional expectations.
- Estimation: regress the residualized outcome variable on the residualized causal variable of interest.
We have no strong priors on whether a linear or non-linear learner is more appropriate, or whether regularization is needed at all. Hence we use 3 learners in this example: unregularized OLS, cross-validated Lasso, and a random forest. We also use model averaging to combine the estimated conditional expectations from these 3 learners. Specifically, we use short-stacking which is a computationally cheap and fast way of pairing DML and model averaging (see Ahrens et al. (2025) for a description of the algorithm and other model averaging strategies). Also to make the example run quickly the initial estimation is done just once, i.e., we do not resample (repeat the cross-fit based on different splits).
The dataset is small, and so we choose 10-fold cross-fitting. This means that learners are trained on about 66-67 observations, and OOS predictions are obtained for the remaining 7-8 observations. (If the dataset were larger, we could e.g. use 5-fold cross-fitting and save some computation time.)
Stata code
// In the G-N estimations, GDP is missing for one country.
// For simplicity, we just drop this one country so that it is never used.
drop if loggdp==.
// To make the code more readable, define macros Y, D and X:
global Y A198new
global D sd_EE
global X v104_ee settlement_ee polhierarchies_ee loggdp
// In Stata, we use the ddml package along with the pystacked package.
// pystacked is a front-end to sklearn's stacking regression.
which ddml
which pystacked
// Step 1: Specify the model.
// We use the partially-linear model with 10-fold cross-fitting and a single cross-fit split.
ddml init partial, kfolds(10) reps(1)
// Step 2: Choose the learners.
// We use unregularized OLS, cross-validated lasso and random forest.
// We use the same learners for Y and X for expositional simplicity only.
ddml E[Y|X]: pystacked $Y $X ///
|| method(ols) ///
|| method(lassocv) ///
|| method(rf) ///
, type(reg)
ddml E[D|X]: pystacked $D $X ///
|| method(ols) ///
|| method(lassocv) ///
|| method(rf) ///
, type(reg)
// Check that the learners have been entered correctly.
ddml desc, learners
// Step 3: Cross-fit.
// We use short-stacking to combine the conditional expectations
// of the different learners.
// The default behavior of ddml+pystacked is to do standard stacking,
// which is computationally intensive; short-stacking is faster.
// To suppress standard stacking, we use the nostdstack option.
ddml crossfit, shortstack nostdstack
// Step 4: Estimation
// After Step 3, we have 4 sets of residualized Y and 4 of residualized D,
// based on 4 sets of estimated conditional expectations:
// one for each of the 3 learners plus one stacked (ensemble) estimate.
// By default, ddml reports the short-stacked results:
// the residualized dependent variable Y is regressed on the residualized
// causal variable of interest D using OLS.
// Note that if you execute the code your your results will vary
// (usually only slightly) because the seed hasn't been set.
ddml estimate, robust
Stata output
. ddml estimate, robust
Model: partial, crossfit folds k=10, resamples r=1
Mata global (mname): m0
Dependent variable (Y): A198new
A198new learners: Y1_pystacked
D equations (1): sd_EE
sd_EE learners: D1_pystacked
DDML estimation results:
spec r Y learner D learner b SE
ss 1 [shortstack] [ss] -2.164 (0.741)
Shortstack DDML model
y-E[y|X] = y-Y_A198new_ss_1 Number of obs = 74
D-E[D|X] = D-D_sd_EE_ss_1
------------------------------------------------------------------------------
| Robust
A198new | Coefficient std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
sd_EE | -2.16408 .7413585 -2.92 0.004 -3.617116 -.711044
_cons | .0000172 .052501 0.00 1.000 -.102883 .1029173
------------------------------------------------------------------------------
Stacking final estimator: nnls1
R code (to be added)
R code here
R output (to be added)
R output here
Seed
We deliberately haven’t set the random number seed here to so that you can re-run the results multiple times and to illustrate how the results will vary based on the randomization of the cross-fit split and any randomization used by the learners.
Typically the DML short-stacked results are quite close to the original linear specification use by G-N. A natural interpretation is that the G-N results still stand in this robustness check. This does not mean, however, that the linear specification was the “right” choice. Depending on the randomization in the cross-fit split and the learners, the short-stacking weights will typically put a low weight on unregularized OLS. The random forest learner will also typically get a substantial weight in both of the conditional expectation estimates. This suggests that some nonlinearity is present, but that the assumption of linearity does not substantially affect the results.
Stata code
// Display the short-stack weights.
ddml extract, show(ssweights)
Stata output
. ddml extract, show(ssweights)
short-stacked weights across resamples for A198new
final stacking estimator: nnls1
learner mean_weight rep_1
ols 1 2.176e-19 2.176e-19
lassocv 2 .48057557 .48057557
rf 3 .51942443 .51942443
short-stacked weights across resamples for sd_EE
final stacking estimator: nnls1
learner mean_weight rep_1
ols 1 0 0
lassocv 2 .41567395 .41567395
rf 3 .58432605 .58432605
R code (to be added)
R code here
R output (to be added)
R output here
Results by learner
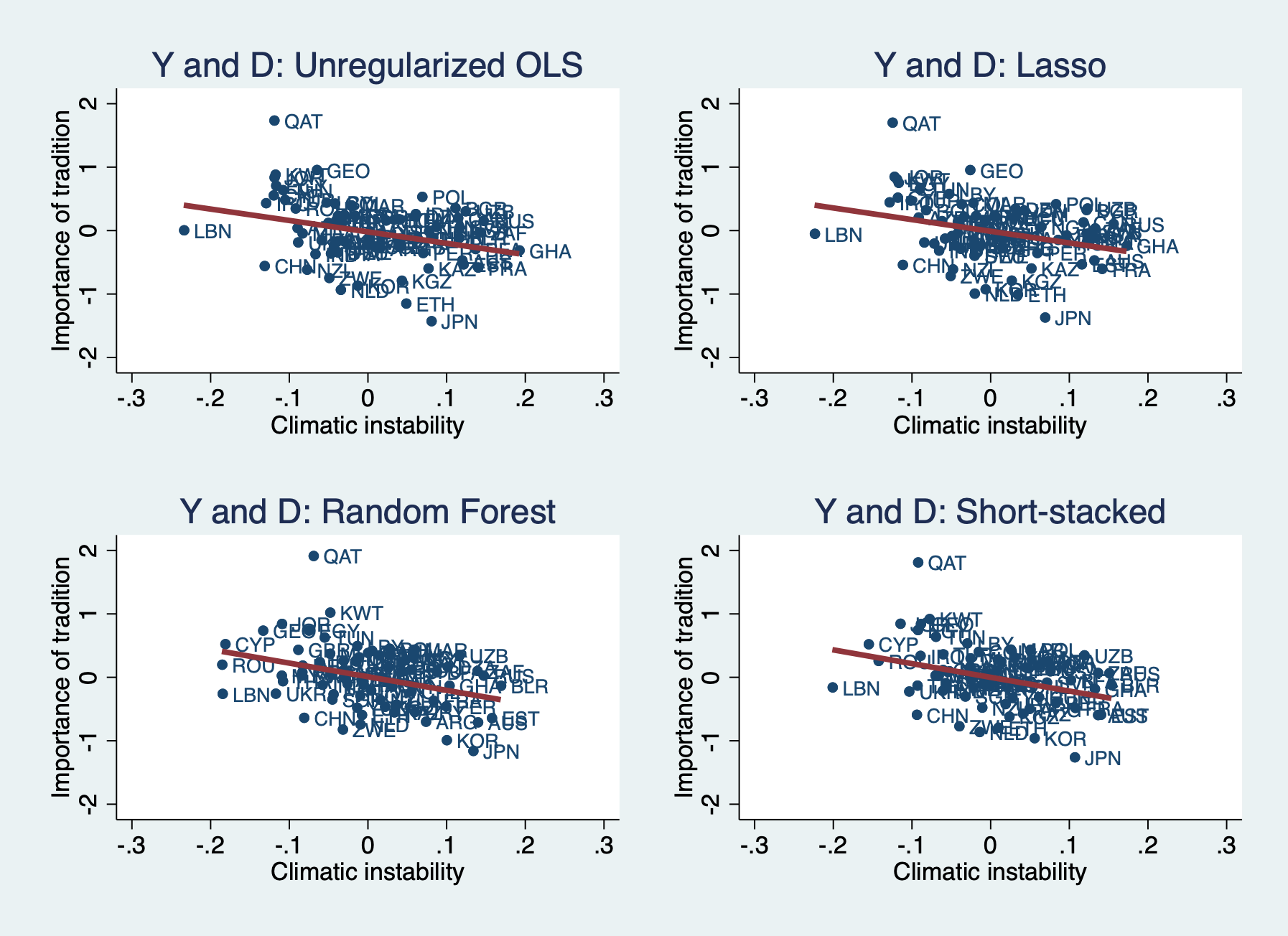
The residualized $Y$ and $D$ can also be inspected and used in other specifications. The G-N dataset is very small and we can plot the results as in Figure 5 of the original paper. Below we look at scatterplots where the same learner is used for both $Y$ and $D$. But we could also look at combinations, e.g., unregularized OLS for $Y$ and RF for $D$. This is related to a version of stacking sometimes called “single-best”, where instead of deriving weights using NNLS, all the weight is put on the learner with the best OOS performance (smallest MSPE).
Stata code
// ddml creates conditional expectations for each learner.
// With pystacked, the learners are numbered.
// The final "_1" identifies the resample (the single cross-fit split).
// Create residualized Y and D for each learner.
cap drop Y_L1_r Y_L2_r Y_L3_r Y_ss_r D_L1_r D_L2_r D_L3_r D_ss_r
gen Y_L1_r = $Y-Y1_pystacked_L1_1
gen Y_L2_r = $Y-Y1_pystacked_L2_1
gen Y_L3_r = $Y-Y1_pystacked_L3_1
gen Y_ss_r = $Y-Y_A198new_ss_1
gen D_L1_r = $D-D1_pystacked_L1_1
gen D_L2_r = $D-D1_pystacked_L2_1
gen D_L3_r = $D-D1_pystacked_L3_1
gen D_ss_r = $D-D_sd_EE_ss_1
// 4 specification and scatterplots
// Y and D learners = OLS
// We suppress the output for the individual OLS regressions to save space.
qui reg Y_L1_r D_L1_r, robust
est store ddml_L1_L1, title("OLS learners")
cap drop hat_1_1
predict hat_1_1
twoway (scatter Y_L1_r D_L1_r, msymbol(o) mlabel(isocode)) ///
(line hat_1_1 D_L1_r, sort lwidth(thick)), ///
legend(off) ///
xlabel(-0.3 -0.2 -0.1 0 0.1 0.2 0.3, nogrid) ///
ylabel(-2 -1 0 1 2, nogrid) ///
title("Y and D: Unregularized OLS") ///
ytitle("Importance of tradition") ///
xtitle("Climatic instability") ///
name(OLS, replace)
// Y and D learners = CV Lasso
qui reg Y_L2_r D_L2_r, robust
est store ddml_L2_L2, title("Lasso learners")
cap drop hat_2_2
predict hat_2_2
twoway (scatter Y_L2_r D_L2_r, msymbol(o) mlabel(isocode)) ///
(line hat_2_2 D_L2_r, sort lwidth(thick)), ///
legend(off) ///
xlabel(-0.3 -0.2 -0.1 0 0.1 0.2 0.3, nogrid) ///
ylabel(-2 -1 0 1 2, nogrid) ///
title("Y and D: Lasso") ///
ytitle("Importance of tradition") ///
xtitle("Climatic instability") ///
name(Lasso, replace)
// Y and D learners = Random Forest
qui reg Y_L3_r D_L3_r, robust
est store ddml_L3_L3, title("RF learners")
cap drop hat_3_3
predict hat_3_3
twoway (scatter Y_L3_r D_L3_r, msymbol(o) mlabel(isocode)) ///
(line hat_3_3 D_L3_r, sort lwidth(thick)), ///
legend(off) ///
xlabel(-0.3 -0.2 -0.1 0 0.1 0.2 0.3, nogrid) ///
ylabel(-2 -1 0 1 2, nogrid) ///
title("Y and D: Random Forest") ///
ytitle("Importance of tradition") ///
xtitle("Climatic instability") ///
name(RF, replace)
// Y and D learners = Short-stacked (ensemble of OLS, Lasso, RF)
qui reg Y_ss_r D_ss_r, robust
est store ddml_SS_SS, title("SS learners")
cap drop hat_ss_ss
predict hat_ss_ss
twoway (scatter Y_ss_r D_ss_r, msymbol(o) mlabel(isocode)) ///
(line hat_ss_ss D_ss_r, sort lwidth(thick)), ///
legend(off) ///
xlabel(-0.3 -0.2 -0.1 0 0.1 0.2 0.3, nogrid) ///
ylabel(-2 -1 0 1 2, nogrid) ///
title("Y and D: Short-stacked") ///
ytitle("Importance of tradition") ///
xtitle("Climatic instability") ///
name(SS, replace)
// Compare DML estimations for learner combinations:
// nb: Code uses estout by Ben Jann; install from SSC Archives.
estout ddml_L1_L1 ddml_L2_L2 ddml_L3_L3 ddml_SS_SS, ///
label modelwidth(15) collabels(none) ///
rename (D_L1_r D_r D_L2_r D_r D_L3_r D_r D_ss_r D_r) ///
cells(b(fmt(3)) se(par fmt(3))) ///
varlabels(_cons Constant)
// Compare via scatterplot:
graph combine OLS Lasso RF SS
Stata output
. // Compare DML estimations for learner combinations:
. // nb: Code uses estout by Ben Jann; install from SSC Archives.
. estout ddml_L1_L1 ddml_L2_L2 ddml_L3_L3 ddml_SS_SS, ///
> label modelwidth(15) collabels(none) ///
> rename (D_L1_r D_r D_L2_r D_r D_L3_r D_r D_ss_r D_r) ///
> cells(b(fmt(3)) se(par fmt(3))) ///
> varlabels(_cons Constant)
------------------------------------------------------------------------------------
OLS learners Lasso learners RF learners SS learners
------------------------------------------------------------------------------------
D_r -1.799 -1.839 -2.147 -2.164
(0.665) (0.668) (0.680) (0.741)
Constant -0.020 -0.011 0.010 0.000
(0.055) (0.055) (0.054) (0.053)
------------------------------------------------------------------------------------
R code (to be added)
R here
R output (to be added)
R output here
Final model
The procedure above is suitable for “work-in-progress”.
For “final” results (e.g., for publication), a researcher should:
- Set the random number seed(s) for replicability.
- Consider using multiple cross-fit splits and aggregate them.
- Check if results are robust to the number of cross-fitting folds.
- Validate the choice of machine learner, e.g., by inspecting cross-validate loss measures or through model averaging approaches such as short-stacking.1
Cross-fitting introduces randomness by using a random split into cross-fit folds. A straightfoward way to reduce the sensitivity of the results to the split is to re-estimate using different cross-fit splits and aggregate the results. Aggregation can use the median or the mean.
The example below illustrates.
Stata code
// "Final" results:
// 1. Set seed for replicability.
// 2. Report all 3 stacking methods.
// 3. 11 separate cross-fit splits and median aggregation.
// The choice of 11 separate cross-fit splits is so that the median is well-defined.
// Set the seed.
set seed 42
// Step 1: Specify the model.
// Use 11 separate resample splits.
ddml init partial, kfolds(10) reps(11)
// Step 2: Choose the learners.
// Conditional expections are defined as before.
ddml E[Y|X]: pystacked $Y $X ///
|| method(ols) ///
|| method(lassocv) ///
|| method(rf) ///
, type(reg)
ddml E[D|X]: pystacked $D $X ///
|| method(ols) ///
|| method(lassocv) ///
|| method(rf) ///
, type(reg)
// Step 3: Cross-fit.
// We focus on short-stacking for this illustration.
ddml crossfit, shortstack nostdstack
// Step 4: Estimation.
// Median-aggregated short-stacked results are reported by default.
ddml estimate, robust
Stata output
. // Step 4: Estimation.
. // Median-aggregated short-stacked results are reported by default.
. // We also ask for the standard and pooled-stacking results.
. ddml estimate, robust
Model: partial, crossfit folds k=10, resamples r=11
Mata global (mname): m0
Dependent variable (Y): A198new
A198new learners: Y1_pystacked
D equations (1): sd_EE
sd_EE learners: D1_pystacked
DDML estimation results:
spec r Y learner D learner b SE
ss 1 [shortstack] [ss] -2.326 (0.802)
ss 2 [shortstack] [ss] -1.907 (0.769)
ss 3 [shortstack] [ss] -2.141 (0.723)
ss 4 [shortstack] [ss] -2.058 (0.790)
ss 5 [shortstack] [ss] -2.265 (0.797)
ss 6 [shortstack] [ss] -2.108 (0.764)
ss 7 [shortstack] [ss] -2.252 (0.735)
ss 8 [shortstack] [ss] -1.892 (0.733)
ss 9 [shortstack] [ss] -1.941 (0.749)
ss 10 [shortstack] [ss] -2.231 (0.735)
ss 11 [shortstack] [ss] -1.911 (0.763)
Mean/med Y learner D learner b SE
ss mn [shortstack] [ss] -2.094 (0.774)
ss md [shortstack] [ss] -2.108 (0.767)
Shortstack DDML model (median over 11 resamples)
y-E[y|X] = y-Y_A198new_ss Number of obs = 74
D-E[D|X] = D-D_sd_EE_ss
------------------------------------------------------------------------------
| Robust
A198new | Coefficient std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
sd_EE | -2.108401 .7674987 -2.75 0.006 -3.612671 -.6041313
------------------------------------------------------------------------------
Stacking final estimator: nnls1
Summary over 11 resamples:
D eqn mean min p25 p50 p75 max
sd_EE -2.0937 -2.3256 -2.2521 -2.1084 -1.9105 -1.8915
R code (to be added)
R here
R code (to be added)
R output here
The median results from the 11 DML estimations are again similar to the original G-N results. The conclusion is again that their specification is robust to dropping the linearity assumption.
Note that the variation across the 11 refits introduced by the randomization of the cross-fit split is not trivial - the DML coefficient estimates range from about -1.7 to about -2.3 - but not enough to overturn the conclusion above. Increasing the number of refits is worth considering here.
It’s also still the case that there is evidence of nonlinearity: all 3 stacking procedures tend to put a low weight on unregularized OLS. Now the nonlinear random forest learner typically gets the biggest weight. Again, this is evidence of some nonlinearity, but not enough to overturn the OLS-based results. (Below we only show the short-stacking weights for the sake of brevity.)
Stata output
. // Display the stacking weights.
. // As before, unregularized OLS gets a low weight for both Y and D,
. // and the random forest learner gets a substantial weight in both.
. ddml extract, show(ssweights)
short-stacked weights across resamples for A198new
final stacking estimator: nnls1
learner mean_weight rep_1 rep_2 rep_3 rep_4 rep_5 rep_6 rep_7 rep_8 rep_9 rep_10 rep_11
ols 1 .2780639 .25021548 .44603695 .15314268 .68821837 0 8.412e-18 .11566583 .08583231 .34503221 .49644733 .47811173
lassocv 2 .15544152 1.031e-18 .11247891 .3152944 1.086e-19 .49763273 .31023968 .1796082 .28357956 0 1.952e-18 .01102318
rf 3 .56649459 .74978452 .44148413 .53156292 .31178163 .50236727 .68976032 .70472597 .63058813 .65496779 .50355267 .51086509
short-stacked weights across resamples for sd_EE
final stacking estimator: nnls1
learner mean_weight rep_1 rep_2 rep_3 rep_4 rep_5 rep_6 rep_7 rep_8 rep_9 rep_10 rep_11
ols 1 1.490e-18 0 0 3.209e-18 0 6.072e-18 3.326e-18 1.502e-18 0 0 2.277e-18 0
lassocv 2 .33170229 .37136168 .34520346 .32768056 .27627495 .3283087 .38245886 .40774365 .37568256 .26729688 .30843848 .25827545
rf 3 .66829771 .62863832 .65479654 .67231944 .72372505 .6716913 .61754114 .59225635 .62431744 .73270312 .69156152 .74172455
R output (to be added)
R output here
-
Short-stacking stacking is computationally appealing but there are other options. Standard stacking - stacking separately for each cross-fit estimation - is also a possibility. “Pooled stacking” is similar to standard stacking except that the weights for combining learners are based on the OOS predictions for the entire sample (rather than for each cross-fit fold separately). See the discussion in Ahrens et al. (2025). ↩